Uncertainty in Machine Learning
Some things in life are certain - for instance, we tend to take for granted that the sun will rise every day. Similarly, everyone knows that each Christmas, Canadian-Italian singer-songwriter Michael Bublé will emerge from his secret hideaway and top Christmas playlists yet again.
9 min read
·
By Bendik Witzøe
·
December 12, 2019
However, other things are not so certain. Today, we will take a look at how uncertainty may play a role in how we interpret machine learning models.
###Black Box versus White Box Models
As modern machine learning models become able to solve increasingly challenging problems, their application has grown tremendously. In the US, deep learning patent applications grew on average by 175% annually between 2013 and 2016. This has caused an ever-expanding range of complex models.
One challenge with the complexity of modern deep learning models is the non-trivial task of understanding precisely why a model produces the outputs it does. Deep learning models may have millions of model parameters and determining the values is not an exact science. Once trained, understanding the complex relationship between inputs and outputs can be extremely difficult. In other words, many modern models exhibit traits of a black box. In black box models the relationship between inputs and outputs is not easily interpretable – it’s as if we are dealing with a black box which magically gives us answers given our inputs.
Conversely, in white box models we can clearly understand and explain the relationship between inputs and outputs, and thus also model behaviour.
So why can black box traits be problematic? There are several reasons:
- Transparency: Certain applications require a business to be transparent about its conduct. For instance, Norwegian insurance companies are required by law to be able to document why a customer was given a higher than average premium on their car insurance. This is not possible if the premium is the output of a black box deep learning neural network.
- Interpretability: As data scientists, we are often more concerned with how a deep learning model performs than we are with the exact science of the underlying algorithm. However, if you know your deep learning model in a critical application you are able to also improve on other parts and be able to critically evaluate why the model performs as it does.
- Explainability: As practitioners of machine learning, we try to solve real world problems. In many cases, deep learning models support human decision making or are applied in settings where the end user may not be a data scientist. Usually, we see that the level of trust in a machine learning application increases with our ability to explain a model’s behaviour in human terms. And if your model isn’t trusted by its users, it may never actually be put in production.
The debate of which is superior between white and black box models is not something we will dive into in this blog post – but we will look at how we can utilize uncertainty to assist in both interpretability and to some extent explainability.
###About uncertainty
Uncertainty in the setting of modelling a problem comes in two forms:
- Aleatoric uncertainty refers to irreducible uncertainty in the variables or data we are trying to model. Consider a model which predicts the outcome of throwing a dice – no matter how many data points we gather, there is inherent uncertainty in the outcome which we cannot reduce. In fact, aleatoric stems from Latin aleator, meaning dice player.
- Epistemic uncertainty is often called model uncertainty and refers to the uncertainty that we have chosen the correct model for our problem. This uncertainty is reducible given more data. Using our dice throw prediction model again, let’s say we are given data points for throws of 2, 3 and 5. At this point, a careful data scientist knows that there is a possibility the data was generated by an 8-sided dice. However, if we are given 1 million data points and all fall between 1 and 6, we are confident the 6-sided dice is the right model – the epistemic uncertainty is reduced to virtually 0.
Thus, for every prediction a model makes we deal with both aleatoric and epistemic uncertainty, in sum comprising what is often referred to as prediction uncertainty. As a side note, if we consider humans to be deep learning models in action, we also deal with the same uncertainties. Below is the picture of “The Dress”, a picture which went viral because people couldn’t agree on what colours they see (spoiler: it really is black and blue). We’ll leave it to the reader to determine if this is aleatoric or epistemic uncertainty – or both!

###Uncertainty in a Machine Learning Problem
Let’s look at the two types of uncertainty in the context of a simple regression problem. Here we have some data points in two dimensions, and we wish to model the output y as a function of x. We have fitted a deep learning model to the data (a simple model would have sufficed for this problem, but the discussion scales to higher dimensions and more complex problems).
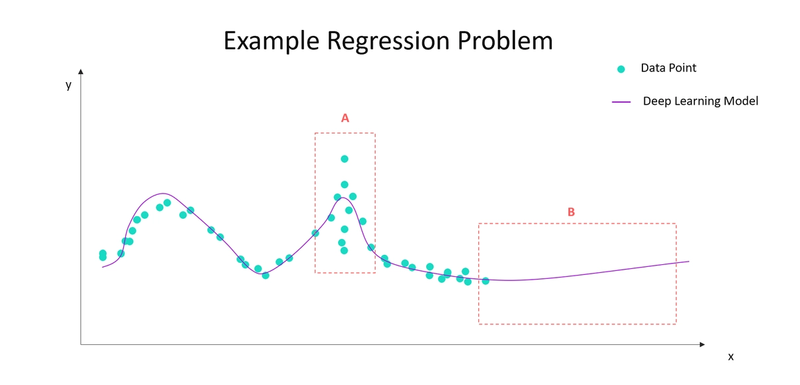
Our model seems to fit the data reasonably well, but there are two areas of particular interest.
In area A, it seems we have several values of y for similar x. Perhaps our data stems from an inconsistent sensor, or we are even missing a third-dimension, z, which could explain this behaviour. However, if we assume that we cannot repair our sensor or measure more dimensions – we are dealing with high aleatoric uncertainty in this area. Ideally, we would want the model to tell us that on average its prediction will be fairly accurate, but real values of y may deviate more in area A than in its immediate neighbouring spaces.
In area B, we lack data altogether. Yet, if we ask our model what it predicts for y in this area, it will give an answer. Now you might object that in the same way you wouldn’t ask your dentist for advice on stock trading, you shouldn’t ask this model what y is for unseen x. However, in real applications we may not always be able to guarantee this doesn’t happen – consider for instance an autonomous car image recognition system seeing an object for the first time. In area B, we are very uncertain that we have the right model and the epistemic uncertainty is high. However, given some more data in this area, we could reduce it. Here, we would want the model to say (like the dentist would): “I’ll give you an answer if you force me to, but honestly I have no idea”.
Clearly, while uncertainty will not improve the performance of our model by itself, it will help with explaining and predicting the behaviour of the model. In areas with high prediction uncertainty, we expect our model to be wrong more often – traits which by themselves are not explained by traditional performance metrics. Effectively communicating this can improve trust in a system even though performance remains constant.
Now that we have identified these uncertain areas, let’s briefly look at how we can estimate the uncertainty and communicate it using deep learning models.
###Estimating Uncertainty
Data scientists with a penchant for the Bayesian school will argue that you should always model uncertainty because it is always present in any problem. However, we can often afford to overlook it if the application is not critical. In cases that you do need to consider uncertainty, several approaches exist. A thorough review is beyond the scope of this blog post, but we will give some pointers for those who are interested.
For epistemic uncertainty, we will highlight two approaches:
- Ensemble methods: This approach works by training an ensemble of models, with randomness either in parameters or the learning process leading to slightly different fits. Treating these models as a distribution then lets us estimate the epistemic uncertainty. As a generic approach, this works for any model for which there is a randomness to the training process.
- Dropout: Dropout is a technique typically applied during the training of deep neural networks, where neurons are randomly dropped each iteration to increase robustness to overfitting the data. However, it was recently shown that dropout can be used at evaluation time to approximate model uncertainty. Thus, instead of an ensemble of models we use small variations of the same model to estimate epistemic uncertainty. See the excellent blog post by Yarin Gal below for the derivation and interactive examples:
For the aleatoric uncertainty:
- Learning the aleatoric uncertainty: Under some assumptions on how noise in the data behaves as a function of the input variables, we can modify the loss function of our model to include an estimate of the aleatoric uncertainty. For image recognition where a model learns the depth, i.e., the distance to objects, we can output higher aleatoric uncertainty for objects with blurred boundaries or objects that are seemingly very far away. For regression, we can output our prediction as a distribution with a mean and variance.
Also, worth mentioning is the study of using machine learning to produce prediction intervals for regression problems which is concerned with outputting intervals with a given confidence level that the real value will be contained within the interval. Some approaches do not require assumptions on the underlying distributions of the data.
###Does This Mean a Free Lunch?
Finally, we should point out that in data science, there is no free lunch. This also applies to estimating uncertainty in deep learning models, which comes at a cost:
- The complexity of a model often increases if we for instance alter loss functions to take into consideration noise in the data. Thus, it may take more time to train models
- Ensemble methods and the dropout approach require several iterations at test time, which means it can take longer time to run models and obtain predictions
- Some approaches require assumptions regarding the nature of the aleatoric uncertainty, which may be difficult to justify in complex settings where we do not understand the data well enough
We encourage you to remember that uncertainty is always present in deep learning models, so determining when you need to take it into consideration is a valuable skill as a data scientist.
Up next...
Loading…
Loading…
Loading…
Loading…