A history of beer, statistics and pseudonyms

I am of course talking (writing) about the t-test. The test that has come to be a useful variation of the Z-test. That’s because where the Z-test makes use of the normal distribution and assumes a large test-sample, not everyone has that luxury and thus there is ample room for the t-test that relies on the students t-distribution. But I’m getting ahead of myself, lets go back to the beginning, to 1908.

Willam Sealy Gosset was a chemist working at Guinness Brewery in Dublin, Ireland. Here he was tasked with, amongst other things, quality control of the beer. To do this he measured sugar content in the malt extract – too high sugar content would mean higher taxes, but too low and the alcohol percentage in the finished beer would be too low. By talking samples of the beer, he could use the normal distribution and Z-test to determine if the batch he was testing was outside the normal range.

However, he had a problem. For the test to be valid he required a large sample size, because as he noted - “… the greater the number of observations of which means are taken, the smaller the error”. But this would mean taking away too much beer that should rather be sold. Preferable he should be able to test the quality of the beer with as few as two samples.

Gosset realised that with small sample sizes there was not errors, but even our estimate of the standard error had noise in it, causing a bias in the absolute values in the distribution. To account for this bias he created a new distribution that flattens the normal distribution and thus moves cut-off scores outwards.

At the time Gosset published his findings under the pseudonym “student” in order to be allowed to publish his findings. In 1912, mathematician Ronald Fisher discovered a mistake in the distribution and added a correction that said that the total sample size, n, should be reduced by 1, and it was at this time that the distribution became known as The Student’s T-distribution.

###The t-test

There are many variations of the T-test, depending, depending on the specific scenario your using it for, and if it’s a one-tailed or two tailed test. The following formula is for comparing two means to see if they are different from each other. Here it is assumed that the variance of the two datasets are similar.

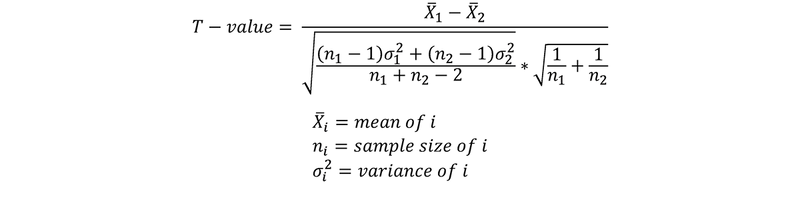
Try using this formula the next time you conduct an AB-test to verify that your results are statistically significant!