Smoothing Out Noisy Signals Using Discrete Mollifier Transforms

Time-dependent data may only be sampled at discrete points in time, thus producing a discrete sequence of observations. Such a time-sampled sequence is usually referred to as a time series.

Examples of time series include electrocardiograms (ECG) from hospital patients and name popularity trends over time, the first of which is discussed in more detail below. Other examples include digital audio signals, the evolution of stock prices, et cetera.

Sampling continuous phenomena over time is not always smooth sailing. The famous Shannon–Nyquist theorem is a classical example providing sufficient conditions on the sampling rate of a signal, that is, the number of samples per second, to avoid such effects as aliasing; it tells us that sampling at a rate twice that of the highest frequency occuring in the signal will be sufficient.

Another challenge presented to us is noise. Even if the underlying phenomenon being sampled is of a continuous, or even smooth, nature, the procedure of sampling a signal generally introduces noise as an artefact on top of the true signal which one wants to capture – measured data which is not really there.

It is therefore natural to ask if it is possible to remove the noise and recover the true, underlying signal. Many such techniques do indeed exist, and the noise reduction filters presented here were developed by the author when he was working as a summer intern on the Pacertool project at Simula Research Laboratory in the summer of 2019.

During the summer of 2019 at Simula Research Laboratory, the author was tasked with the creation of tools for automated analysis of ECG signals. This entailed in part the automatic detection of QRS complexes in such signals.

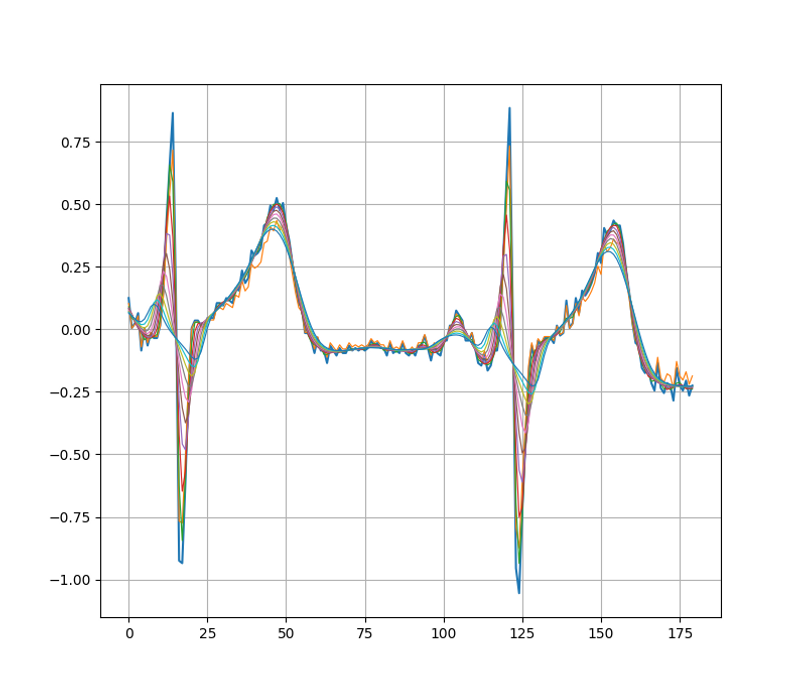
An ECG signal is produced by placing electrodes on the patient's limbs and chest to record the electrical activity of their heart, thereby producing a waveform of the type which is here exemplified by public data from WFDB:

An algorithm for automatic QRS detection in ECG signals must be able to precisely pinpoint the onsets (Q) and offsets (S) of the complex, a task which is readily seen to be complicated by the presence of noise. Indeed, signal spikes produced by the noise may fool the algorithm into premature onset or offset detection, or even into thinking there is a QRS complex where there is none.

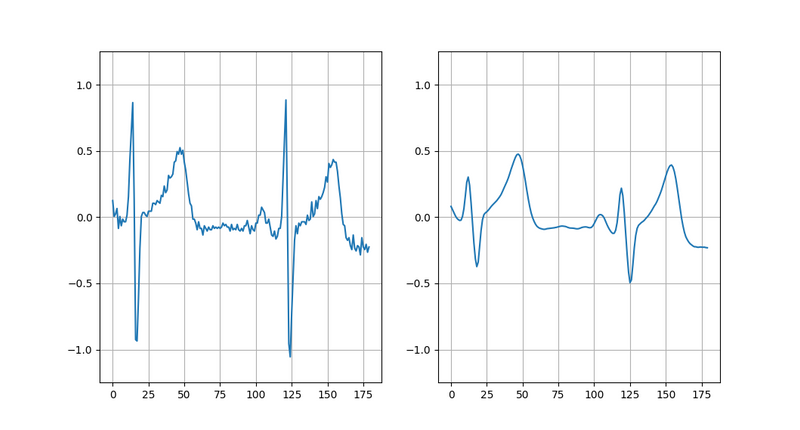
A common remedy is to preprocess the signal by smoothing out noise before pinpointing the complexes, here achieved by the discrete mollifier transform to be studied in more detail in part two of this series:

There are plenty of situations where noise reduction of time series data is desirable, and the techniques for doing so are well within reach for anyone with minimal programming experience. Here we had a brief look at situations where noise reduction is beneficial. In the next article, we take a mathematical and technical look at how the particular class of discrete mollifier transforms used above are defined, implemented, and how they relate to other common regularization operators. See you there!